Helping to grow OLBG and support our partnerships with Harry Derham Racing & Dorking Wanderers FC
Ever wonder how to maximise your betting wins? In this informative article, we guide you through the best staking plans for betting, truly a game-changer for anyone keen on boosting their success rate ay betting sites.
You will discover many tactics and strategies that seasoned professionals utilize, all aimed at optimising your odds and transforming your betting journey.
Transform Your Betting Skills with our Staking Guide!
What Is A Staking Plan?
A Staking Plan is setting a monetary budget that you always adhere to when placing bets. The Staking Plan dictates how much of your money you bet on individual wagers in your betting bank. This can also include using free bets as part of your strategy.

Betting Banks
Professional punters like to have a set betting bank (size varies depending on wealth) from which they place all their bets.
This allows them to easily keep track of profit and loss because all winnings and losses are coming from the same bank.
It also allows them to stake set proportions of their bank on bets which reflect their confidence in the selection's chances.
Scattergun Approach
Profit from the bank is periodically withdrawn or withdrawn when it reaches a certain amount to be used for non-betting purposes.
Selecting winners and taking the best prices from the best betting sites will naturally help grow the bank.
So we now have a Staking Plan and the money we use comes from our Betting Bank.

Any free bets or bookmaker promotions can be used alongside your staking plan and added to your betting bank. Particularly look out for major event. Ryal Ascot for example, or use the huge number of Cheltenham Free bets that are available when the festival coms around.
Types Of Staking Plan
Level Stakes
This is the most common of the Staking Plans - you bet the same amount on every selection.
It could be £1 or £10 or 1% or 5% of your betting bank.

To test out this staking plan go to the horse racing tipping pages and add the same monetary amount for every selection.
Test it for a month and see if a profit can be made:
Kelly's Criterion
Kelly's Criterion is a formula that is used to determine how much of a bank should be risked on a given bet.
The formula takes into account the odds of the bet and the probability that it will win and the probability that it will lose.
This does have the advantage of ensuring the whole bank is never lost on a bet and helps to steadily increase the bank.
A disadvantage of this is that there is no way of guaranteeing that money won't be lost.
In fact, there is a 1/3 chance of halving the bankroll before it is doubled.
| Stake Calculator | |
| Your Betting Bank | |
| Chance of Winning | |
| Best Odds (decimal) | |
| Suggested Stake | |
OLBG Blogger Garethp1981 has written a blog about this staking plan, he asks Does Kelly Have The Answer.
Whilst OLBG Editor In Chief Steve Madgwick looked at How To Maximise Profit And Minimise Loss on Horseracing with Kelly Criterion.
Martingale System
The Martingale System is often associated with Roulette but can be applied to any sort of betting.
It is essentially doubling up after every losing bet.
If the odds are evens or over then in theory the punter cannot lose as they will receive all of their losses back every time they back a winner.
However, in this theory the punter has an unlimited betting bank to cover each bet.
In reality betting banks can run out and maximum stakes that bookies will allow can be exceeded so the Martingale system is not recommended as the stakes can soon get out of control.
Example of the Martingale System
- You bet £1 and lose so you bet £2 but that loses.
- So you bet £4 and that loses too.
- So you bet £8 and that wins.
- You make £8 profit on your final winning bet which after the previous 3 losses of 1,2 & 4 = £7, leaves you with £1 profit.
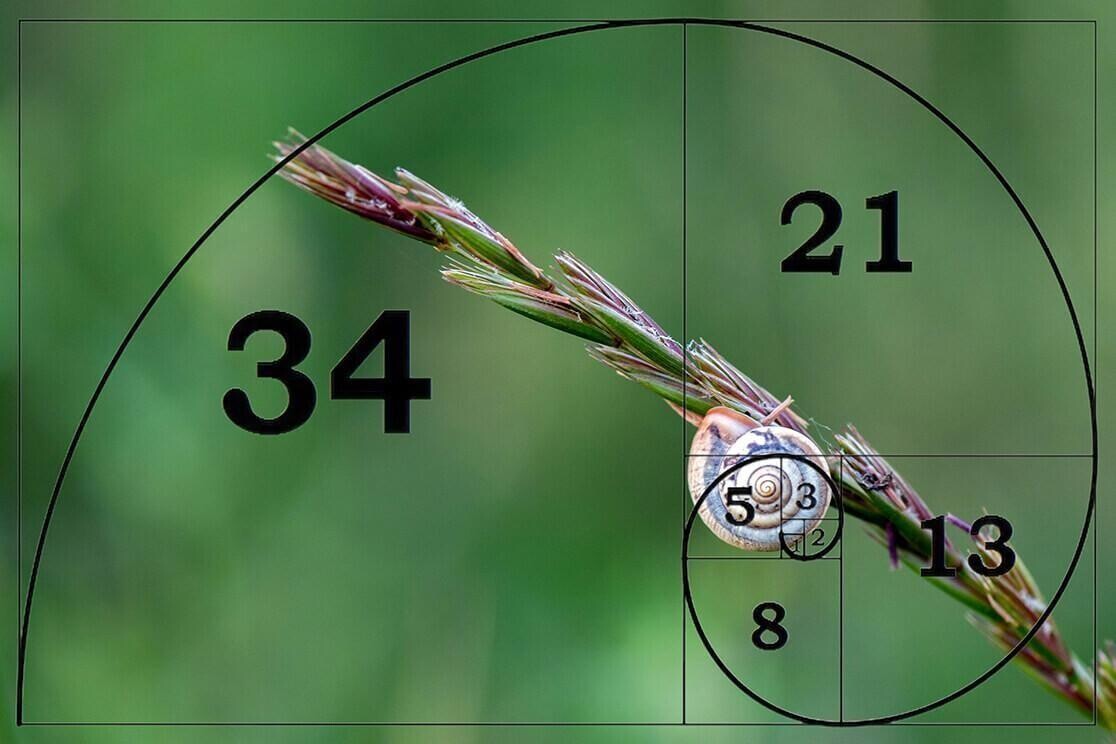
Fibonacci staking
A Fibonacci staking plan in horse racing is a strategy where you adjust your betting amount based on the Fibonacci sequence ( 1, 1, 2, 3, 5, 8, 13, 21)
Fibonacci was a 12th-century Italian mathematician who solved a problem using a set of numbers; this became known as the Fibonacci sequence.
Determine your initial betting amount, let's say it's £1.
Start with your £1 on your first bet.
After each bet:
If you win, go back two steps in the sequence.
If you lose, move one step forward in the sequence.
- £1
- £1
- £2
- £3
- £5
- £8
- £13
- £21
For example, If the first five bets in the sequence are losers and the £8 bet wins, you return to £3.
| Sequence | Bet | Result | Profit and Loss | Running Total |
| 1 | £1 | Lose @2/1 | -£1 | -£1 |
1 | £1 | Lose @2/1 | -£1 | -£2 |
1, 2 | £2 | Lose @3/1 | -£2 | -£4 |
1, 2, 3 | £3 | Lose @9/2 | -£3 | -£7 |
1, 2, 3, 5 | £5 | Lose @4/1 | -£5 | -£12 |
1, 2, 3, 5, 8 | £8 | Win @ 2/1 | 16 | £4 |
Despite the five losers you created a profit with your sixth bet.
If you were betting to level stakes you would be sitting on a loss, by using Fibonacci you are in profit.
Obviously your selection process needs to be decent and helps you recover losses in a systematic way, remember though it can lead to needing to place large bets after a series of losses.
Other Staking Systems
It can often be better to change this system slightly to take into account confidence.
Three levels of confidence can be assigned, with 7.5% of the bank being a confident bet, 5% being an average bet and 2.5% being a not so confident bet.
You could name them
- (Nap) = 7.5%
- (NB) = 5%
- (Standard Bet) = 2.5%
The exact percentages used are of course up to you.
An OLBG member a few years back wrote about his Cheltenham Staking Plan.
He uses this at many of the the big horse racing festivals, it involves Win & Place bets and Lucky 15 wagers and is worth checking out.
Stakes and Bank
You may have a betting bank of £100 or £1000 the amount is not important.

You would divide your bank into small units or bigger chunks and then once you had reached say £200 or £2000 you would withdraw the profit or some of the profit, and start again from £100 or £1000.
You could set either a monthly target or a date in the future and then start again.
Unit Stakes
Assigning unit stakes to bets can be useful as it makes the punter more disciplined and less likely to over bet an event.
Sometimes a maximum and minimum unit stake is used, from one unit to twenty units for example.
Depending on the seriousness of the punter a unit may be £1, £10, £100 or even more.
These units are usually referred to as points, a £1 could be one point or £10 could be one point
So three points on a selection would either be £3 or £30.
The more disciplined a punter the smaller band of units they will probably use.
This makes them even less likely to over or under bet an outcome as the difference in confidence between units will be even more clearly defined in their mind.

Recovery Staking To A Target Plan
Staking Notes
The key to managing money is to bet sensibly.
The main rule every punter should have is to only ever bet what they can afford to lose.
Betting should be viewed as fun more than anything else and when it is no longer fun it is probably time to give it up.
Betting an entire bank is never a good idea either.
However confident you may be about an outcome, freak results do happen and it can leave you with nothing left with which to try and claw your losses back.

Responsible Gambling Features, Function and Help
Chasing Losses
The biggest mistake someone can make is to chase their losses.
Chasing losses is when someone tries to win back what they have lost in a day or week by either upping their stakes or betting on selections they wouldn't normally gamble on.
The best way to avoid chasing is to set out exactly how much you are going to bet on your fancied selections at the start of a day and preferably what prices you expect
Stick to this rigidly and there shouldn't be any problems.
If you find that you are one of those people that just can't help chasing your losses then place your bets in the morning and don't check the results until that night when all the racing or football matches have finished and there is nothing else to bet on.

Discipline and Gambling. Not that again?
Chance Versus Odds
A good way of determining how confident you are about a bet and therefore how much you should stake on it is to consider how many times you think that outcome would occur if the event was run or played ten times.
The more times it should happen the better the bet is.

Converting Odds To Probability
Then you have to consider value so consider how many times you think the event will occur and compare it to the odds available.
Something that you would expect to happen five times out of ten but is only a 4/5 shot is not a good a bet
Something you would only expect to happen one time out of ten but is a 33/1 shot is a good bet.
The better the chances seem compared to the odds available, the more units should be assigned to the bet.
Example
FAIR ODDS: If the horse is priced at even money.
5 wins @ Evens = 5 points profit, but 5 losses =-5 => (Break Even).
BAD ODDS: If the horse is priced at 1/2.
5 wins @ 1/2 = 2.5 points profit, but 5 losses =-5 => - (2.5 loss of our 10 staked).
GOOD ODDS: If it was priced at 3/1
5 wins @ 3/1 = 15 points profit, but 5 losses =-5 => (10 profit from 10 staked.).
Staking Plans FAQ
FAQ
Staking Plans FAQ
What is a Staking Plan?
It is a method that enables you to understand how much money you should risk when placing a bet.
You follow this plan at all times so your staking is consistent.
Why should I use a Staking Plan?
- It helps you manage and stay in control of your bankroll.
- It minimises you losing all your funds.
- It stops you from making impulsive or emotional decisions.
Can I bet different amounts using a Staking Plan?
It really depends on your plan; the key is to adhere to the plan despite the temptations of doing otherwise.
What Staking Plan is right for me?
As a bettor, are you risk averse (I am)?
There are varying degrees of this based on your financial situation and personal preferences.
Choose the staking plan based on your tolerance to risk and reward.
How Much Should I Start A Staking Plan With?
As mentioned above, the size of your bankroll is not important.
Just make sure that you have enough funds to give the Staking Plan a chance to prove its worth.
Will Staking Plans work for Exchange trading?
The principle is the same whether you are betting or trading. You may lay horses to a fixed amount or back football teams to win a certain percentage.